【摘 要】新课标提出了“设计体现结构化特征的课程内容”的课程理念,在这一背景下,数学教师在钻研教材时,除要吃透教材的编写意图外,还要运用“求联”思想对教材内容进行结构化分析处理。具体可在规划蓝图、结构选材、关联立序、精选题组等环节分别采取“本质统领·一脉相承”“任务驱动·好材支撑”“联结推进·整体建构”“围绕模块·结构组题”等策略,促使学生在联结性学习活动中展开联结思考,获得结构化理解,实现整体建构。
【关键词】小学数学 分析教材 处理策略 结构化 “求联”思想
《义务教育数学课程标准(2022年版)》(以下简称“新课标”)印发之后,“有关联地学”成为重要的学习方式之一。想促进学生有关联地学,教师就要开展有结构地教。因此,结构化的联结教学成为落实新课标理念的有力抓手。基于“求联”的结构化教学是一项系统工程,包含的内容很多,其中结构化分析处理教材属于该工程的开端,也是一个前提性要素。 数学教师在充分读懂教材编写意图的基础上,根据“求联”思想进行审视,寻找新知内容所属整体的共同本质,在本质沟通下进行该整体的系统规划,在整体蓝图的统领下,对教材的每一部分内容进行结构化处理,为学生提供具有结构化特征的课程内容,进而引领学生展开联结性学习。下面以北师大版数学五年级下册“确定位置(一)”为例,谈一谈结构化分析处理教材的具体策略。
“求联”视角下结构化钻研教材,要从“整体”出发,要把每一棵“树”(一节课)放到整个“森林”(一个板块)中去审视,因为每一棵“树”都是 在“森林”这个大环境中生长的,大环境的状况对它有很大影响[1]。因此,在钻研某一节课的教学内容时,教师首先要去研究该内容所在的整体结构,弄清整体与部分、部分与部分之间的内在关联,提炼出各子要素之间的共同本质,以共同本质(联结点)为统领,布好“整体蓝图”,并在分段实施时做到“孕伏在先、一脉相承、不断进阶”,以结构联结的力量促使学生展开整体建构学习[2]。
“确定位置(一)”是北师大版数学五年级下册第六单元第一课时的内容,属于图形与几何领域中的“方向与位置”板块,该板块共包含四个部分,分别是“认识上下前后左右”“认识八个方向”“用数对确定位置、能看懂简单路线图”“根据方向和距离确定位置”。该板块的核心素养目标是空间观念中的“想象并表达物体的空间方位和相互之间的位置关系”[3]。结构化钻研教材,要先对本板块的整体结构做个剖析。该整体对平面上的方向与位置的确定采取了逐步缩小范围的策略:从“区域”到“线”到 “点”,即从描述某一大范围的方向(上下左右、八个区域方向),到定格在某条“线”上的方向(用四个正方向或象限角描述的方向),再到精准定位在某个“点”的位置(用数对确定位置,或根据方向和距离确定位置)。本课时已经推进到了“在平面上确定某个点的位置”这个阶段了。前两个阶段的经验是本节课进一步学习的基础。本阶段内容的本质是:在同一平面内两线的交点能确定一个唯一的位置。这个本质(联结点)统领着本节课的所学内容和之前学过的“用数对确定位置”的内容。因此,规划完这一板块的整体蓝图后,在“用数对确定位置”那个阶段,就要对本质要素进行孕伏性运用。本节课在前面的基础上展开一脉相承的进阶:根据相同点进行结构化迁移—两线交点确定一个位置;抓住不同点进行结构化辨析—由“两射线的交点”发展为“曲线和射线的交点”。根据上述分析,本节课的着力点就是做好与之前已学的“用数对确定位置”的求联沟通与结构迁移,争取形成合力,获得整体建构的效果。
二、进行“结构选材”:任务驱动·好材支撑
想使结构化联结教学有效发生,就要给学生提供结构化的材料和求联性的任务,促使学生展开联结性探究活动[4]。好的结构化材料是支撑学生联结性思考活动有效发生的引擎。北师大版数学教材的编写体系是“情境+问题串”,情境体现的是主题任务,问题串是完成任务的主要思路。教师在钻研教材时要吃透编者的意图,在此基础上进行结构选材的审视:如果教材已经具备了结构化任务驱动的功能,就选用教材上的内容作为联结性学习的素材;如果教材上的材料结构化不强,可以对教材进行二次开发,另行设计更好的结构化学习材料来支撑和驱动联结性探究活动的开展。
“确定位置(一)”的主题情境是动物园各馆的路线图(见图1)。
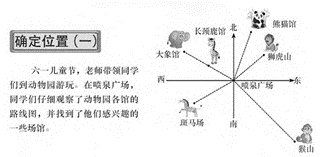
图1 北师大版数学教材中的情境图
教材中分别安排了三个问题串:①熊猫馆在喷泉广场的什么方向?②大象馆和长颈鹿馆都在喷泉广场的北偏西60。的方向上,如何区分它们的位置呢?③参观斑马场后,同学们想去猴山,说一说他们的行走路线。根据前面对本课内容本质要素的分析,教师发现教材上的材料基本上还是具有结构化特征的。主题情境作为总的任务驱动,引出探究的内容;问题串中的第一个问题解决“带角度的方向(象限角)”这个要素;第二个问题解决“距离”这个要素;第三个问题通过起点的变化厘清“观测点”这个要素。这样的结构选材,基本上能促使学生实现对新知的建构。当然,在完成任务方面,要想起到更大的诱发驱动作用,教师在导入时可增设以下材料。
一艘游轮在茫茫的大海上航行,突然遇到一股强烈的台风,迷失了方向。更糟糕的是船底撞到了暗礁,游轮被撞出了好几个窟窿,游客们惊慌失措,形势十分危急。冷静理智的船长立刻请求救援,海上救援队接到救援信息,马上派出救援船舰和飞机,及时精准地到达了事故地点进行施救,大家才躲过一劫。
了解情况后,让学生说说救援队为什么能这么快速而精准地到达出事地点,从而诱发学生产生探索确定位置方法的欲望。
三、展开“关联立序”:联结推进·整体建构
分析处理教材的两个核心任务是选材和立序。在前一个环节确定了所用素材之后,怎样把这些素材用好用活还是一门技术。一方面,要遵循认知活动动态进阶的规律,动态使用静止的材料;另一方面,要从“求联”视角出发,对学习材料进行关联立序。首先,大环节上要围绕结构本质要素搭建“联结支架”[5],在整体架构上体现出联结推进的逻辑序列。其次,在 每个环节内,要对选用的结构化材料展开联结性探究活动。最后,要安排一个归总梳理活动,通过引导学生对整个探究活动进行联结性反思,实现整体建构。
“确定位置(一)”这节课可整合教材原有内容,安排以下几个联结性探究活动。
(1)回顾“用数对确定位置”的方法,出示方格图,以喷泉广场为原点(0,0),确定熊猫馆的位置是(2,5),并带领学生总结出“用数对确定位置” 的方法,即确定好原点后,用纵横(纵轴与横轴)两条射线的交点确定一个唯一的位置。
(2)只用一条信息描述熊猫馆的位置,信息有: ①东北;②北偏东20°;③距离喷泉广场900米。让学生把自己想象成站在喷泉广场上,面向北方,然后从三个信息中选一个来描述熊猫馆的位置,可分别得出“在一个区域内”“在一条射线上”“在一个半径为 900米的圆上”三个结论。
(3)选用若干条组合信息描述熊猫馆的位置,可分别发现:①+②的组合缩小了范围,但只知在“射线”上,不能确定位置;①+③的组合只知在某个小区域的“曲线”上,也不能确定位置;②+③能确定熊猫馆所在的唯一位置(射线与曲线的交点);①+②+③能确定唯一位置,但有多余信息。
(4)改变观测点来描述位置:参观斑马场后想去猴山,怎么描述行走路线?体会观测点的重要性和相对性,并总结出用这种方法确定位置的基本要素。
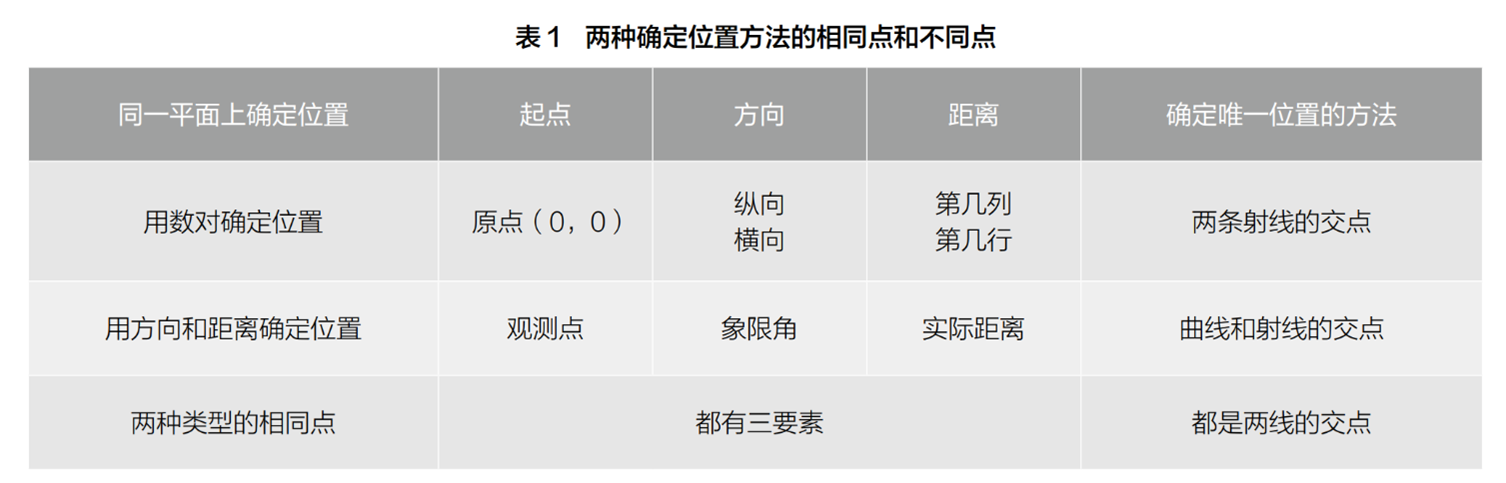
(5)联结梳理:本节课所讲确定位置的方法和“用数对确定位置”的方法有什么相同点和不同点? 通过联结性反思进行总结提炼(见表1)。
四、精选“题组练习”:围绕模块·结构组题
分析处理教材既包含教材上新知学习的部分,还包括练习巩固的部分。教师要深入分析教材中的练习部分,理解题目编排的意图,弄清练习进阶的层次和每道题所巩固的知识点。在此基础上,按照“求联”思想进一步审视教材上的题目及编排顺序是否具有结构化特征。如果教材内容体现得不明显,可重新设计题组练习。结构化的练习是以模块题组为载体,以精巧的结构进行优题组合,取得“1+1 > 2” 的训练效果[6]。要设计好结构化练习,首先要精准掌握所学新知模块的本质要素,然后围绕模块本质要素进行结构组题,可以把教材上的和自行创编的题目结合起来。
“确定位置(一)”这节课,教材上安排了四道练习。第一大题是告诉方向和距离(有3个组合供选择),在方位图上选择相应组合填出位置;第二大题是提供方位图上的地点信息,要求写出三个地点的方向和距离;第三大题是用本节课的新增知识从正向和反向来描述行走路线;第四大题是实践游戏,两个学生互相看对方,用观测点的不同体验方向描述的不一样。前面两道大题是基础性练习,从正向和逆向两个视角来巩固“方向和距离”这两个基本要素,第四大题是体验“观测点”这个要素,第三大题是将本节课所学知识与以前所学的路线图进行综合应用。教材这样安排,基本起到了巩固的作用, 但从联结性视角去审视,还缺少一些结构化辨析的题组。这节课知识的本质是“用曲线和射线的交点确定一个位置”,围绕该模块本质可为学生设计一组逐步进阶的对比辨析的结构化练习:(1)方向相同但距离不同的多个位置的同异辨析题;(2)距离相同而方向不同(不同方向的可用对称形式,便于比较)的多个位置的对比辨析;(3)提供不同方向(象限角也用两种方式表示)和不同距离以及不同观测点的多个信息,根据指定的位置来组合选择三要素信息(组合的种数比较开放和多元)。总之,力求通过这些分层渐进的结构化题组训练,使学生对新知本质有一个深度认识。
本文从四个维度探讨了“求联”视角下结构化分析处理教材的一些策略,既尊重教材,充分理解教材的编写意图,又创造性地开发教材,给学生提供结构化的学习内容,搭建起具有导航引领作用的联结支架,促使学生的联结性思考活动和结构化理解有效发生,最终达到整体建构的目的。当然,文中谈的策略只是一部分,实际上远不止这些。只要教师怀着结构化的思想和联结意识去探索,一定能找到更多有效分析处理教材的策略和方法。
参考文献
[1] 席爱勇,何杰.结构关联:小学数学结构化学习的学理探究——以《小数的意义》为例[J].淮阴师范学院学报(自然科学版),2018,17(4):355-359.
[2] 陈力.数学结构化教学中“联结点”的动态进阶织网策略[J]. 教学与管理,2023(32):42-45.
[3] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[S]. 北京:北京师范大学出版社,2022:9.
[4] 陆泉萍.求联驱动:催化数学理解的自然进阶[J].数学学习与研究,2021(8):120-122.
[5] 陈力.小学数学“联结课堂”的三个基本要素特征[J].中国教师,2024(4):65-69.
[6] 陈力.以模块题组为载体的“结构化练习”设计与应用[J].小学教学设计,2022(29):10-12.
本文系浙江省教育科学规划课题“数学‘联结课堂’:践行系统观念的学科育人探索”(立项号:2025SC130)核心成果之一。
(作者系:1﹒浙江省武义县熟溪小学校长,高级教师;2﹒浙江省武义县教育局教研室教研员,正高级教师)
责任编辑:赵继莹
